※ 위상 순서
1. 부분 순서(partial order)
i) 이행적(transitive), 비반사적(irreflexive)인 선행관계일때, 관계 R은 부분 순서라고 한다.
ii) 집합S, 관계R에서 S의 원소 i, j, k :
①R은 S에서 이행적이라면 -> iRi&iRk이면 iRk가 성립 ②비반사적일때->모든 i가 iRi가 성립하지않음
iii) 이행적이면서 대칭적(symmertric)이라면 부분 순서 성립x: 이 관계는 반사적이고 반사적이면 부분 순서가 성립x
iv) DAG(Directed Acyclic Graph): 비반사적 그래프는 싸이클이 없고 이를 DAG라 한다.
2. 위상 순서(topological order)

i) 정의: 방향그래프에서 정점 i가 선행자이면 i > j 순서를 가진 순차리스트
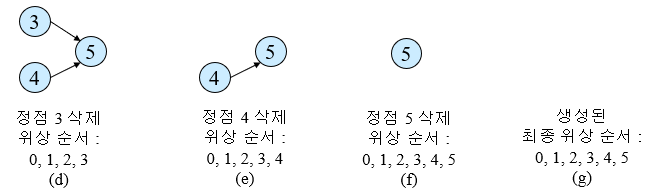
ii) 위상 정렬 알고리즘
topologicalSort(AOVnetwork, n)
// G=(V,E), n=|V|
for(i<-0; i<n; i<-i+1) do{
select u with no predecessor;
if(there is no such u) then return;
print(u);
remove u and all arcs incident from u;
}
iii) 위상 순서를 위한 인접리스트 구조: 기존 인접리스트에 indegree 필드 추가(진입차수의 개수)

※ 임계 경로
1. AOE(Activity On Edge) 네트워크: 프로젝트 스케줄을 표현
i) 장점: 프로젝트 수행을 위한 공정단계
ii) 간선: 공정들의 선후 관계와 각 공정의 작업 소요 시간
2. 임계 경로(Critical Path): 시작점에서 완료점까지 시간이 가장 많이 걸리는 경로
3. EC(i)(Earliest Completion time) 공정 Pi의 조기완료시간: 시작점부터 공정 Pi까지 최장 경로 길이

EC(6)=12
a. P0->P1->P6: 길이 4 + 5 = 9
b. P0->P2->P4->P5->P6: 길이 2+1+2+5=10
c. P0->P3->P5->P6: 길이 3+4+5=12 => EC(6)
4. LC(i)(Latest Completion time) 공정 Pi의 완료마감시간: 영향을 주지 않고 공정 Pi가 여유를 가지고 지연하여 완료할 수 있는 시간
- (전체 프로젝트 완료 시간) - (공정 Pi가 최종공정까지 최장 경로 길이)
5. 임계 경로 계산
① 공정 조기 완료 시간( EC(j) ) 계산: AOE 네트워크 위상 순서로 계산
- weight(i,j) =작업시간, EC(0)=0
- EC(j) = max{ EC(i) + weight(i, j), j로 진입하는 모든 i}

② 공정 완료 마감 시간( LC(i) ) 계산: AOE 네트워크 위상 순서 반대로 계산
- LC(n-1)=EC(n-1)
- LC(i) = min{ LC(j) - weight(i, j), i에서 진출하는 모든 j}

③ 작업 임계도( CR(i, j) ) 계산: CR(<i, j>) = LC(j) - (EC(i) + weight(i, j))

④ 임계 작업: 임계 경로 상에 있는 작업( 작업a<i, j>: EC(i) = LC(i)이고 EC(j) = LC(j)인 작업)
- 네트워크에서 임계도가 0인 임계 작업만 남기고 제거하는 작업

임계 경로:
0-> 1-> 5-> 6
0-> 3-> 5-> 6
'알고리즘' 카테고리의 다른 글
| [Algorithm] 히프 정렬 (0) | 2022.11.22 |
|---|---|
| [Algorithm] 퀵 정렬 (0) | 2022.11.22 |
| [Algorithm] MCSP_최단거리 (0) | 2022.10.26 |
| 알고리즘 시험공부) 힙 (0) | 2022.10.17 |
| 알고리즘 시험공부) 이진탐색 트리와 연산 (0) | 2022.10.17 |
