1. 그래프를 인접 리스트로 표현

import java.util.Stack;
class Graph{
Node header[] = new Node[10];
boolean visited[] = new boolean[10];
public void Graph(){
for(int i=0; i<10; i++)
visited[i] = false // 방문 안함으로 초기회
} // end of contructor
public void build(){
header[0] = new Node(0, new Node(1, new Node(3)));
header[1] = new Node(1, new Node(0, new Node(2, new Node(3))));
header[2] = new Node(2, new Node(3)));
header[3] = new Node(3, new Node(1, new Node(2))));
}
public void display(int n){
//인접 리스트로 표현
Node m = header[n];
while(m!=null){
System.out.println(m.data+" ");
m = m.link; // 다음노드로 이동
}
}
}2. 깊이 우선 탐색(DFS) 수행


public int DFS(int m){
int j;
static int NumberOfNodes = 7;
boolean visited[]= new boolean[10];
for(j=0; k<NumberOfNodes; j++)
visited[j]=false;
Stack<Integer> a = new Stack(); // 스텍 생성
a.push(m); // n을 push
while(!a.isEmpty()){ // a가 빌때까지 수행
j = a.pop() // 스택 a의 pop해준 값을 j에 삽입
Node node = header[j]; // 노드 하나 선언
if(visited[j] == false){ // 노드 방문 시 false일때
System.out.print(node.data+" "); // visit j
visited[j] = true;
for(;node != null; node = node.link){
a.push(node.data); // 노드가 null일때까지 노드 데이터를 push
}
}
}
}3. 너비 우선 탐색(BFS) 수행


public int BFS(int m){
boolean visited[] = new boolean[10];
for(int i=0; i<10; i++)
visited[i] = false;
ListQueue q = new ListQueue(); // 방문할 정점을 저장할 큐
Node n = header[m];
q.enqueue(n); // m 정점을 인큐
while(!q.isEmpty()){
Node p = (Node) q.dequeue(); // 디큐하고 순회포인터 가르킴
if(visited[p.data] == false) { // 디큐하지 않았다면 방문 후 기록
System.out.print(p.data+" "); // visit j;
visited[p.data]=true;
}
while(p.link != null){ // 바로 옆 정점이동
p = p.link;
if(visited[p.data] == false) // if(visited[k]=false) then
q.enqueue(header[p.data]); // enqueue(queue, k)
}
}
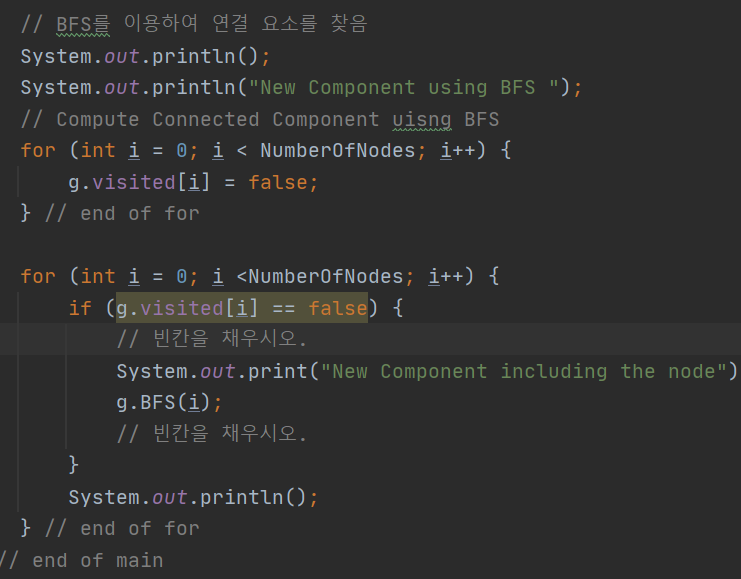
}4. 연결 요소


'알고리즘' 카테고리의 다른 글
| 알고리즘 시험공부) 힙 (0) | 2022.10.17 |
|---|---|
| 알고리즘 시험공부) 이진탐색 트리와 연산 (0) | 2022.10.17 |
| [Algorithm]그래프(Graph)의 정의 - 그래프의 순회 (0) | 2022.10.14 |
| [Algorithm]그래프(Graph)의 정의 - 그래프의 표현 (2) | 2022.10.11 |
| [Algorithm]그래프(Graph)의 정의 - 그래프 추상 데이터 타입 (0) | 2022.10.11 |
